Apel :) Matik: Cześć. Mam podobne zadanie jak Nessee, które do pewnego momentu rozwiązał Januszek75 i chciałbym się zapytać czy mógłby je dokończyć bo nie jestem tak błyskotliwy i chyba nie dam sobie sam z tym rady. Przypomnę treść tego zadania. Wyznacz krawędź podstawy ostrosłupa prawidłowego trójkątnego o objętości 2√26, wiedząc, że krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Tutaj jest to rozwiązanie do pewnego momentu "a więc podstawa brył to trójkąt rowoboczny o boku a wysokośc opada z wierzchołka i rowna się H krawędz boczna (jest ich 3emotka ) równa sie b V= 1/3 * Pp * H wysokośc opada na podstawę i dzieli wysokośc podstawy w stosunku 2/3 wysokosc w trojkacie rownoboczny jest h= (√3/2) *a zatem x = (2/3)*h Pp=1/3 * √3/4 *a2 * H b=3*a H2=b2−x2 H2 = 9a2 − 1/3*a2 wylicz z tego H i podstaw do wzoru na V gdzie pole podst. Pp = (√3/4)*a2 2√26 = 1/3 * (√3/4)*a2 * wyliczone wyżej H z tego wyliczysz a" Byłbym bardzo wdzięczny za pomoc

Januszek75: nie rozumiem o co ci chodzi Matki − daj treść zadania

Matik: Wyznacz krawędź podstawy ostrosłupa prawidłowego trójkątnego o objętości 2√26, wiedząc, że krawędź boczna jest 3 razy dłuższa od krawędzi podstawy.

Januszek75: przecież je zrobilem tobie juz − czego nie rozumiesz?

Januszek75: aaaa oki − toż to inne jest trochę − już Ci je zrobię

Matik: Z góry dziękuje

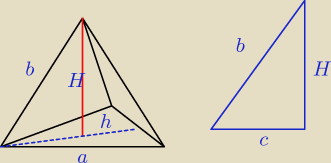
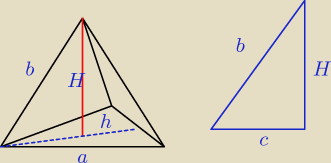Januszek75: b=3a pole podstawy = (√3/4)*a² z wlasności figury winika że wysokosc opada z wierzchołka na podstawe i dzieli ją w sosunku 2/3 stąd c = (2/3)*h ( z niebieskiego trójkąta wylicz H − pitagoras) oraz h = (√3/2)*a do wzory na objetosc 1/3 * P_p * H podstaw wszystko i przekształc tak żeby wyliczyc a